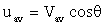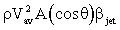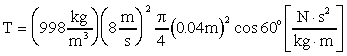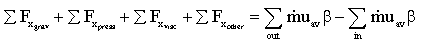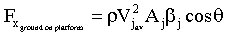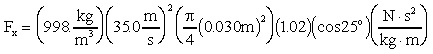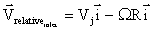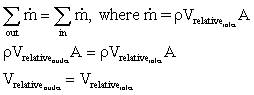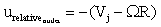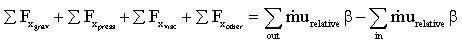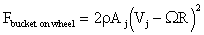Conservation of Momentum using Control Volumes
Conservation of Linear Momentum
Recall the conservation of linear momentum law for
a system:

In order to convert this for
use in a control volume, use RTT with B = mV, beta
= V
we get:

NOTE: Recall that at any instant of time t, the system
& CV occupy the SAME physical space.
So, the forces of the system are the same at the
forces of the control volume at a given instant.
Example Problems
Given: A water jet of velocity Vj and thickness Dj impinges on a turning block which is held in place by a force Fx, as shown in the sketch.
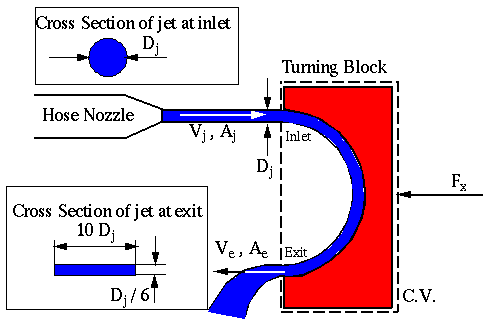
As the water leaves the block, the round jet flattens out and slows down due to friction along the wall. The water turns a full 180 degrees and flattens into a rectangle shape of thickness Dj/6 and width 10Dj in cross section. The flow is steady.
a) Find: Ve, the exit velocity of the jet.
Solution:
- First, pick a control volume which cuts through the inlet and exit, but does not include the turning block.
- Use conservation of mass for steady 1-D flow:

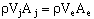
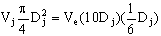
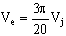
b) Find: Fx, the force required to hold block in place.
Solution:
- Choose a new control volume because friction along the wall would be very hard to evaluate with the previous C.V. Pick a C.V. which cuts through the inlet and outlet and that includes the whole turning block. The wisest choice of control volume is one which cuts through where the force Fx acts on the turning block, since Fx is our unknown.
- Write momentum equation for steady 1-D inlet/outlet in the x-direction:
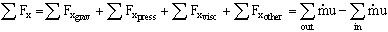
Examine each term on the left:  (no grav in x-dir),
(no grav in x-dir),  (p = pa everywhere),
(p = pa everywhere),  (wise choice of C.V), and
(wise choice of C.V), and 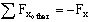
- Thus, the momentum equation reduces to
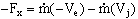
- Now, recall,
 at an inlet or exit. Here at the inlet,
at an inlet or exit. Here at the inlet,
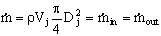
- So, solve for
 :
:
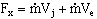
Or, finally,  , which is our final answer.
, which is our final answer.
- Note: This is not merely an academic exercise. A testing facility at NASA Langley Research Center uses this principle to propel a test rig along a track to test airplane landing gear, etc. The experimental facility, called the Aircraft Landing Dynamics Facility, uses a high pressure water jet that hits a turning bucket on the test cart, much like in the above problem. The cart is propelled from zero to 250 miles per hour in two seconds flat!
Momentum Flux Correction Factor
- Again, just like in the conservation of mass equation, even if we don't really have one-dimensional (uniform) inlets and outlets, we would still like to use the simplified version of the conservation of momentum equation. I.e. we would like to use Vav instead of V in the equation.
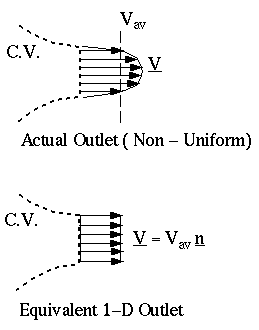
- The equivalent profile and actual profile thus have identical mass flow rates,
 .
.
- What about momentum flow rate, or momentum flux, MF? Do actual and equivalent profiles have the same momentum flux? No! It turns out, after integration, that:
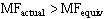
- So, we can't just substitute Vav for V in the momentum equation or we will get the wrong answer. So, instead, let's introduce a momentum flux correction factor,
 :
:
Define: 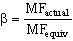
It turns out that:  ,
,
and,  .
.
- Examples:
1) 1-D uniform flow,  by definition
by definition
2) fully developed laminar pipe flow, 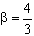
3) fully developed turbulent pipe flow, 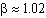
- Now, we can use the one-dimensional form of the momentum equation, but with these momentum flux correction factors thrown in:
For a fixed control volume with steady flow,
 , and
, and 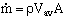
- Fortunately, most problems in real life applications are turbulent, not laminar, and we can usually neglect the momentum flux correction factors since
 is close to 1.0.
is close to 1.0.
Most Useful Form of the Momentum Equation
- For steady flow with a fixed control volume, the most useful form of the momentum equation is thus:
 , where
, where  momentum flux correction factor, and
momentum flux correction factor, and  .
.
Example Problem
Given: Consider incompressible flow in the entrance of a circular tube.

The inlet flow is uniform u1 = U0. The flow at section 2 is developed laminar pipe flow.U0, p1, p2, R, and  , are also known. At section 2,
, are also known. At section 2,  .
.
Find: Total friction force on the fluid from 1 to 2.
Solution:
- First draw a C.V. Again cut through the inlet and outlet 1 and 2. But now, we want to cut along the walls since Ffriction is our unknown.
- Draw all the forces acting on the C.V. in the x-direction.

- Simplifications: Assume steady, incompressible, uniform one-dimensional inlet, but not a uniform one-dimensional outlet.
- So, let's use the modified momentum equation for non-1-D inlets/outlets in the x-direction:
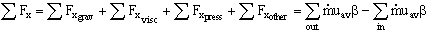
- Now look at each term:
 (no grav. in x-dir)
(no grav. in x-dir)
 (this is our unknown)
(this is our unknown)
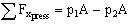
 (no struts, bolts, etc.)
(no struts, bolts, etc.)
 (inlet is 1-D so
(inlet is 1-D so  )
)
 : This term is the hardest. First of all, what is uav? I.e. what is the equivalent 1-D velocity? Well, since the area at the outlet is the same as that at the inlet, uav at the outlet has to equal U0.
: This term is the hardest. First of all, what is uav? I.e. what is the equivalent 1-D velocity? Well, since the area at the outlet is the same as that at the inlet, uav at the outlet has to equal U0.
- What is
 at the outlet? By definition,
at the outlet? By definition,  . You can plug the equation in and integrate [Try it on your own]. You will get
. You can plug the equation in and integrate [Try it on your own]. You will get  (the value for laminar pipe flow).
(the value for laminar pipe flow).
- So, the outlet momentum flux term becomes
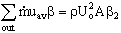
- Finally, then sum everything and solve for the unknown:
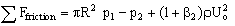
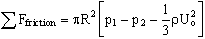
- Notice, if
 is ignored, i.e. (set
is ignored, i.e. (set  ), this last term would cancel completely, and the answer would be wrong.
), this last term would cancel completely, and the answer would be wrong.
More Example Problems
Problem # 3.58 in the text:
Given: Cart with water
jet, deflector, as shown
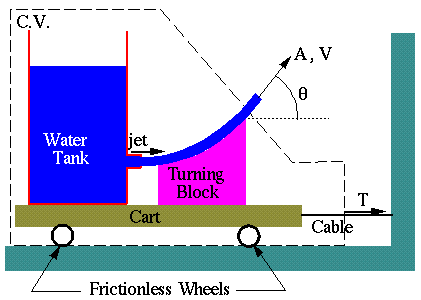
Known in this problem are the jet area A, the average velocity
Vav, the jet deflection angle,  ,
and the momentum. flux correction factor of the jet,
,
and the momentum. flux correction factor of the jet,  .
Also, frictionless wheels are assumed.
.
Also, frictionless wheels are assumed.
Find: Tension in cable
at time t=0.
Solution:
- As always, the first step in any control volume
problem is to pick and draw a control volume. The forces and
coordinate system have been labeled on the sketch. Here it is
appropriate to slice through the jet and slice through the unknown
force T (tension in cable), as shown in the sketch.
- Simplifications:
Incompressible? Yes (water is the fluid, which is approximately
an incompressible liquid)
Steady? - No, not really, since the water level in the tank is
falling. But all we are asked for is T at time t=0, so think
of this as a pseudo-steady problem in order to find T.
Note: The falling water level will have no effect on the x-momentum
equation anyway, since its velocity is vertical.
- Now, use the x-component of the momentum equation
in it steady form:

There is only one outlet, at which
 .
.
The quantity uav in the momentum flux outlet term in
the above equation needs to be considered carefully. This is not
Vav, but rather is the x-component of Vav.
From a little trig one can see that
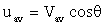
Thus the outlet term on the right hand side of the momentum equation
is
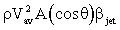
and the final form of the x-momentum equation is (solving for
T):

- Plug in the numbers last: The density of water
at room temperature is 998. kg/m3, the jet velocity,
Vav is 8 m/s, the cross-sectional area A is that of
a circle of diameter 0.04 m, the jet angle is given as 60o,
and the jet momentum flux correction factor is 1.0 for a uniform
jet. This yields:
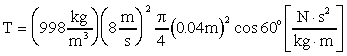
Or T = 40.1 N.
- Question: At what
angle, is the tension a maximum?
Answer: When the jet deflection angle is zero, i.e. the
jet simply exits horizontally into the atmosphere. This is clearly
seen in the above equation since the cosine of zero is unity.
Example A water-mounted fire pump (an old exam
problem.)
Given: A pump is anchored
to the ground as shown, with Vj=35.0 m/s and dj=3.00
cm. Assume the jet has a fully developed turbulent pipe flow profile
at its exit.
picture wat_pump.gif
Find: Horizontal force
required to hold platform in place.
Solution:
- The first step in any control volume problem
is to pick and draw a control volume. As shown, the control volume
should slice through jet exit and through the bolts or whatever
is holding the platform solidly to the ground. The inlet to the
control volume is most easily taken at the surface of the water,
where the pressure and velocity are known (p = pa and
V = 0 at the surface). Note: When this problem was given as
an exam question, lots of students took their control volume inlet
at the pipe inlet. This makes the problem more difficult. Remember
the first rule about selecting a control volume - Be Lazy!
- Apply the x-momentum equation:
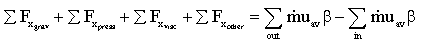
The gravity term on the left hand side is zero because gravity
does not act in the x direction. Likewise, the pressure term is
zero because everywhere on the control surface above the water,
the pressure is atmospheric (including the portion of the control
surface that slices through the jet). Below the water, the pressure
is hydrostatic, and whatever pressure force is exerted on the
left side of the control surface is exactly balanced by that on
the right side of the control surface. In the control volume
selected, there is no net viscous force acting on the control
volume. Thus the first three terms on the left hand side of the
x-momentum equation are zero. The only "other" force
acting on the control surface is the force of the ground acting
on the platform, as shown in the sketch. The direction of this
force is assumed to act to the right; if this is wrong, the result
will be negative.
On the right hand side (the momentum flux terms), there is no
x-component of velocity at any inlet, so the last term on the
right is zero. There is only one outlet, with uav
equal to the x-component of the velocity vector of the jet. Thus,
the x-momentum equation reduces to
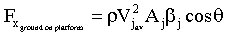
This is the answer in variable form.
- Lastly, plug in the numbers, noting that for
a fully developed turbulent pipe flow the momentum flux correction
factor is around 1.02:
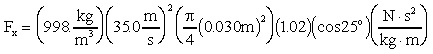
or finally, the horizontal force required to hold platform
in place is 799. N.
Problem # 3.51 in the text:
Given: A turbine wheel,
powered by a water jet, as shown in the sketch (at time t = 0)
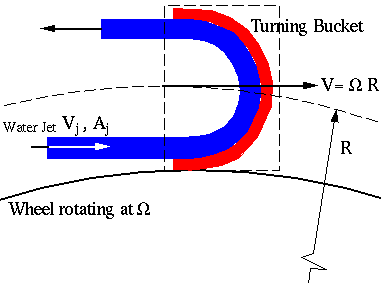
The turbine is spinning at a constant rotational speed.
Assumptions:
- 1-D inlet and outlet
- neglect friction in the turning bucket
(a) Find: The force of the turning bucket
on the turbine wheel at this instant of time.
Solution:
- Pick a control volume. Here we will pick a
moving control volume, which makes things a little tricky.
When the control volume is moving, one must use the relative
velocity, i.e. relative to the moving C.V.
- At the inlet, then, the relative velocity at
the inlet is obtained by subtracting the velocity of the C.V.
from the absolute velocity at the inlet, i.e.
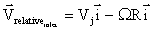
where Vj is the magnitude of the absolute velocity at the inlet,
and its direction is in the positive x-direction. The second
term on the right represents the velocity of the control volume
in an absolute reference frame, which is subtracted as shown.
The x-component of this relative inlet velocity is simply the
magnitude of the above velocity vector, since the vector acts
only in the positive x-direction, i.e.

- Now apply conservation of mass to this moving
control volume. Note: Here, relative velocities must be
used, since they represent the velocities actually entering and
leaving the control volume as it moves along.
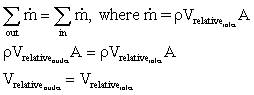
Note that the areas on either side of the equation are identical
by the original assumption of negligible viscous effects. Also
the incompressible assumption causes the density to drop out.
At time t = 0, when the turning bucket is on the top of the turbine
wheel as shown, the velocity of the inlet is in the positive x-direction,
while that of the outlet is in the negative x-direction. Thus,
the x-component of the relative outlet velocity is simply the
negative of that of the relative inlet velocity, i.e.
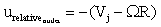
In other words, the turning bucket changes the direction of the
water jet by 180 degrees, but it does not change the magnitude
of the jet velocity. (If friction along the walls of the turning
vane was taken into account, the jet velocity magnitude would
change as well.)
- Now apply conservation of x-momentum
for our moving C.V.
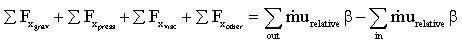
Notice that the relative x-velocity components are used
in the momentum flux terms on the right hand side since this is
a moving control volume. The gravity term on the left hand side
is zero because gravity does not act in the x direction. Likewise,
the pressure term is zero because everywhere on the control surface,
the pressure is atmospheric (including the portions of the control
surface that slice through the jets). In the control volume selected,
there is no net viscous force acting on the control volume. (This
would be true even if viscous forces along the turning vane were
not ignored, because the control surface does not pass along the
turning vane wall.) Thus the first three terms on the left hand
side of the x-momentum equation are zero. The only "other"
force acting on the control surface is the force of the turbine
wheel acting on the turning bucket, which is equal and opposite
to the force of the turning bucket acting on the turbine wheel,
as shown in the sketch. The direction of the force of the bucket
on the wheel is assumed to act to the right; if this is wrong,
the result will be negative.
On the right hand side (the momentum flux terms), there is only
one inlet and one outlet. At both the inlet and the outlet, the
x-component of the relative velocity vector of the jet is known
from the conservation of mass analysis above. Since friction
is being neglected, it is assumed that the momentum flux correction
factors are unity. Thus, the x-momentum equation reduces to

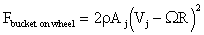
This is the force of the turning bucket on the turbine wheel.
(b) Find: The power, P, delivered to the
wheel at this instant of time (t = 0).
Solution:
- Power on a rotating wheel is defined as the torque
times the angular velocity of the wheel. The torque due to this
turning bucket is the force just derived times the radius fo the
wheel, R. Thus,

(c) Find: The angular velocity which provides
the maximum power to the wheel.
Solution:
- To find the maximum power, take the derivative
of power with respect to angular velocity.

- The values of angular velocity at which this
derivative is zero then represent conditions where the power is
either a minimum or a maximum. There are two such roots, i.e.

- The first of these represents the case where
the absolute jet speed and the speed of the turning bucket are
the same. Under such conditions, no power is transferred to the
turbine wheel at all. (This can be verified easily, i.e. P =
0 when the first root is plugged into the result of part (b) above.)
In other words, the first root is a minimum. The second root
is therefore the desired one; i.e. the angular velocity which
supplies the maximum power to the turbine wheel is that in which
the turbine wheel spins three times slower at its rim than the
jet speed, i.e.
























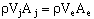
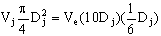
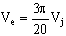
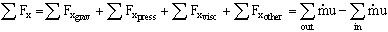
 (no grav in x-dir),
(no grav in x-dir),  (p = pa everywhere),
(p = pa everywhere),  (wise choice of C.V), and
(wise choice of C.V), and 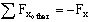
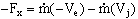
 at an inlet or exit. Here at the inlet,
at an inlet or exit. Here at the inlet, 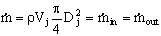
 :
: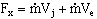
 , which is our final answer.
, which is our final answer. 
 .
. 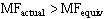
 :
: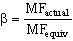
 ,
, .
.  by definition
by definition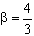
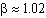
 , and
, and 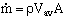
 is close to 1.0.
is close to 1.0.  , where
, where  momentum flux correction factor, and
momentum flux correction factor, and  .
.
 , are also known. At section 2,
, are also known. At section 2,  .
.
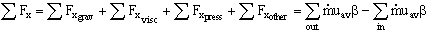
 (no grav. in x-dir)
(no grav. in x-dir) (this is our unknown)
(this is our unknown)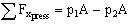
 (no struts, bolts, etc.)
(no struts, bolts, etc.) (inlet is 1-D so
(inlet is 1-D so  )
) : This term is the hardest. First of all, what is uav? I.e. what is the equivalent 1-D velocity? Well, since the area at the outlet is the same as that at the inlet, uav at the outlet has to equal U0.
: This term is the hardest. First of all, what is uav? I.e. what is the equivalent 1-D velocity? Well, since the area at the outlet is the same as that at the inlet, uav at the outlet has to equal U0.  at the outlet? By definition,
at the outlet? By definition,  . You can plug the equation in and integrate [Try it on your own]. You will get
. You can plug the equation in and integrate [Try it on your own]. You will get  (the value for laminar pipe flow).
(the value for laminar pipe flow). 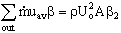
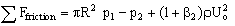
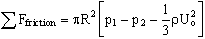
 is ignored, i.e. (set
is ignored, i.e. (set  ), this last term would cancel completely, and the answer would be wrong.
), this last term would cancel completely, and the answer would be wrong.
 ,
and the momentum. flux correction factor of the jet,
,
and the momentum. flux correction factor of the jet,  .
Also, frictionless wheels are assumed.
.
Also, frictionless wheels are assumed.

 .
.