Control Volume (Integral) Technique
Introduction: Techniques for solving flow problems
There are three different techniques for solving these types of problems:
- Control Volume Analysis
- This is just like in thermodynamics class

- One can calculate the gross properties (total power output,
total heat transfer, etc.)
- With this however, we do not care about the details inside the control
volume (In other words we can treat the control volume as a "black
box.")
- Differential Analysis
- In this technique, one solves differential equations of motion everywhere
(i.e. The Navier-Stokes equation).
- Here we solve for all of the details in the flow
- Dimensional Analysis and Experiment
- This method is used when methods one or two are not possible.
- One uses wind tunnels, models, etc. to employ this method.
Introduction to systems and control volumes
System: Consider a system of a fluid:
- Recall from thermo class, that a system is defined as
a volume of mass of fixed identity.
- Let m = the mass of the system
Let V = the velocity of the system
Let a = the acceleration of the system
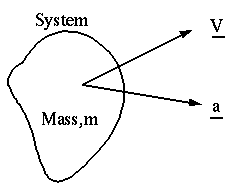
- Now we can write three basic conservation laws which apply to this
system. Note: These conservation laws apply directly to a system.
- Conservation of mass states that the mass of a system
is constant.
This can be written as the following equation:
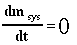
In this equation m = the mass of the system.
- Conservation of linear momentum which is a restatement
of
Newton's Second Law.
- In equation form this is written as:

Where mV = the linear momentum of the system.
- Note that this is the same as Newton's second law, it is just written
a little differently.
- Using the above equation, we can obtain a form of the equation in terms
of acceleration:
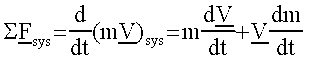
- This equation is obtained through expansion using the product rule.
- We know that ,
 and
and 
by the conservation of mass found above.
- Using these ideas, we can then see that
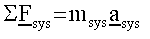
- Conservation of Energy
- For this, use the First Law of Thermodynamics in rate form to obtain
the following equation:

- Where E = the total energy of the system. In the above equation
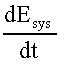
is the rate of change of system energy.
 is the rate of heat added
to the system
is the rate of heat added
to the system 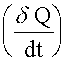
 is the rate of work done
by the system
is the rate of work done
by the system  .
Because work is done by the system, the negative sign is in the equation
for the first law of thermodynamics.
.
Because work is done by the system, the negative sign is in the equation
for the first law of thermodynamics.- Now, these conservation laws must always hold for a system.
- Conservation of Angular Momentum
We will not have time to study this, but see the text for details.
Control Volume:
- One can think of the system approach as the Lagrangian description,
which if recalled is the description where we follow the individual chunks
of the fluid.
- However, the trouble with this is that we prefer to use the Eulerian
Description, where we define a control volume with fluid moving
through it.
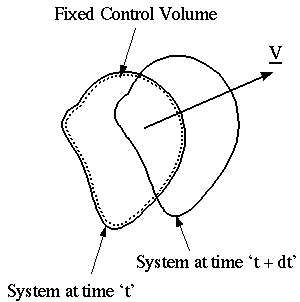
- In other words, if we define some control volume, fixed in
space, the system will flow through it.
- Our goal here is to try to write the conservation laws above in a form
applicable to a control volume (Eulerian description)
rather than to a system (Lagrangian description).
- There is a way to do this, and it is called the Reynolds Transport
Theorem (R.T.T.)
- Now our goal is to write all three of these conservation laws in terms
of a control volume. But, to save us some work, let's not derive it three
times, but just once for a general property B, and then use our
result for any of the three conservation laws:
- In other words, let's write R.T.T. for some arbitrary property B.
Let B = some arbitrary property (vector or scalar) and  per unit mass.
per unit mass.
This way, we can later substitute B for mass, momentum, energy, etc.
- We are then able to make the following substitutions for
 :
:
- For conservation of mass, let B = m, and
 .
.
- For conservation of momentum,
 ,
and
,
and  .
.
- For conservation of energy, B = E, and
 .
.
- SEE the text for the derivation.
REYNOLDS TRANSPORT THEOREM (R.T.T.)
- This is for some property B, and is also for a fixed
control volume.
Deforming the control volume is more complicated; see the text for details.
- The equation for Reynolds Transport Theorem is written as the following:
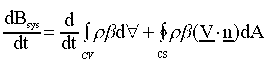
(This is equation 3.12 in the text.)
OR
For a fixed control volume, the order of differentiation
and integration doesn't matter. So alternatively,
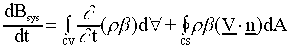
(This is equation 3.17 in the text. )
- Comments on the above equation:
 The total rate of change
of B following the system.
The total rate of change
of B following the system.
This is the term to which the conservation laws directly apply.  The time rate of change
of B within the control volume. This is due to unsteadiness.
The time rate of change
of B within the control volume. This is due to unsteadiness. The net flux of B out of
the control surface.
The net flux of B out of
the control surface.
Due to convection, B changes because system moves to a new
part of the flow field, where conditions are different. A circle
was put around the integral  to emphasize that this is an integral over the entire control
surface. (This is not done in the text however).
to emphasize that this is an integral over the entire control
surface. (This is not done in the text however).
- Sometimes
 and
and  are
used to emphasize that these are volume
are
used to emphasize that these are volume
and area integrals. (Again this is not done in the text).


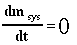

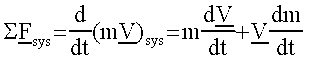
 and
and 
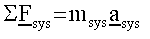

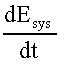
 is the rate of heat added
to the system
is the rate of heat added
to the system 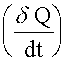
 is the rate of work done
by the system
is the rate of work done
by the system  .
Because work is done by the system, the negative sign is in the equation
for the first law of thermodynamics.
.
Because work is done by the system, the negative sign is in the equation
for the first law of thermodynamics.
 per unit mass.
per unit mass. :
:
 .
.
 ,
and
,
and  .
.  .
.
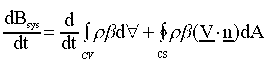
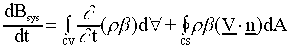
 The total rate of change
of B following the system.
The total rate of change
of B following the system. The time rate of change
of B within the control volume. This is due to unsteadiness.
The time rate of change
of B within the control volume. This is due to unsteadiness. The net flux of B out of
the control surface.
The net flux of B out of
the control surface.  to emphasize that this is an integral over the entire control
surface. (This is not done in the text however).
to emphasize that this is an integral over the entire control
surface. (This is not done in the text however).  and
and  are
used to emphasize that these are volume
are
used to emphasize that these are volume